Starting with normalizing our input features, why do we really need normalizing the input features on the first place? The simple answer is we normalize the input features so that the cost function is elongated so when the gradient descent is run, it makes it easier and faster to find its way to the minimum.
The normalizing inputs are done in two steps:
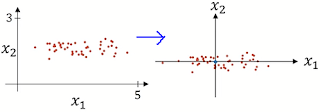
- First , move the training set such as to have a 0 mean
- Second, normalize the variances
The formula for zeroing out mean is:
This makes the training data to set in line like shown:
The second step is normalizing the variances. The formula is:
Vanishing/Exploding Gradients
After normalizing, we'll learn about what vanishing/exploding gradients are.
One of the problems of training neural network especially very deep neural networks is data vanishing and exploding gradients. What this means is that when we are training a very deep network our derivatives or slopes sometimes get either very big or very small, may be even exponentially small and this makes training difficult.
Lets take an example of only two hidden units per layer as shown to understand:
Following equation forms (ignoring b as b=0 )
Now let's say that each of our weight is larger than the identity matrix as shown:
This would mean that Y^ will essentially be 1.5 times the identity matrix to the power of L and multiplied with identity matrix L-1 times X as shown above. So if L is very big in case of a deep neural network the Y^ will be very large. Infact it grows exponentially. Conversely if we replace 1.5 with 0.5, then the activations will decrease exponentially.The same argument of increasing and decreasing gradients goes with the derivatives as well. This problem has a huge barrier for learning deep neural network. However, there is a partial solution to it that exists. We shall now discuss it next.
Partial Solution for vanishing/exploding gradients
The partial solution lies in the more careful selection of the random initialization for your neural network.
Since we want W neither to get too big or too small as was discussed above, one reasonable thing to do is to set the variance such as:
Where n is the number of input features that's going into a neuron. So in practice, what we can do is set the weight matrix W for a certain layer to be:
If we are using ReLU activation function than we can change use the same above formula with a little modification such as the (1/n) is (2/n) in the above formula.
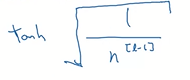
If you use tanh activation function than we use the following formula. It is also called as Xavier initialization.
We can also try this version of formula for tanH activation function:
In practice, all of these formulas just give us a starting point. It gives a default value to use for the variance of the initialization of your weight matrixes.
Gradient Checking
Grad check is a technique that helps save tons of time and find bugs in the implementations of back propagation many times.
Lets see how we use it for debugging or actually verify that our implementation and back propagation is correct.
So to implement grad check, first implement this loop. Note that here we will nudge theta I to add epsilon both sides as we are taking two sided difference.
Once done, we have to see if:
where:
So we are going to compute for every value of i. At the end we end up with 2 vectors which are of same dimension. We see if the two vectors are approximately equal to one another or are reasonably close. For checking we apply the following eucledian distance formula:
We may use epsilon 10x-7 and with this range if we find the check gives:
- < 10x-7 ~ great! correct implementation
- ~ 10x-5 --> needs double checking
- < 10x-3 --> greater chance of implementation is wrong.
Reference:
Andrew Ng coursera https://www.coursera.org/learn/deep-neural-network/lecture/lXv6U/normalizing-inputs
If you enjoyed this post and wish to be informed whenever a new post is published, then make sure you subscribe to my regular Email Updates.
Subscribe Now!
Posts
0 comments:
Leave your feed back here.